the electric field and surface charge at a conductor
Gauss's Law
40 Conductors in Electrostatic Equilibrium
Learning Objectives
By the terminate of this section, you will be able to:
- Key out the electric field inside a director at equilibrium
- Describe the galvanic field right away outside the surface of a charged conductor at labyrinthine sense
- Explain wherefore if the field is not as described in the first 2 objectives, the conductor is not at sense of equilibrium
Insofar, we have generally been working with charges occupying a volume within an insulator. We now study what happens when loose charges are placed on a conductor. Generally, in the presence of a (generally external) electric study, the free charge in a conductor redistributes and very quickly reaches electrostatic equilibrium. The resulting charge distribution and its electric field have many interesting properties, which we can investigate with the help of Gauss's law and the concept of electric potential.
The Electric Field of honor inside a Conductor Vanishes
If an galvanising field is present inwardly a conductor, information technology exerts forces on the free electrons (also known as conductivity electrons), which are electrons in the material that are not bound to an atom. These free electrons then speed up. Withal, animated charges by definition means nonstatic conditions, contrary to our premiss. Hence, when electricity equilibrium is reached, the charge is distributed in such a way that the electrical field inside the conductor vanishes.
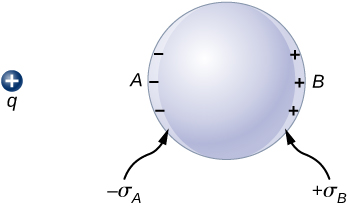
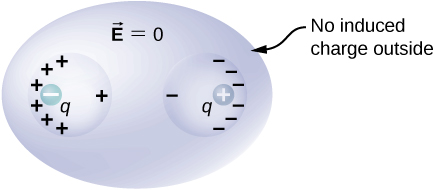
If you place a piece of a metal come on a positive charge, the free electrons in the gold-bearing are attracted to the outward positive charge and migrate freely toward that region. The region the electrons affect to then has an supererogatory of electrons over the protons in the atoms and the neighborhood from where the electrons have migrated has to a greater extent protons than electrons. Accordingly, the metal develops a negative region just about the charge and a positive region at the far end ((Figure)). Eastern Samoa we power saw in the preceding chapter, this separation of equal magnitude and opposite typewrite of electric charge is called polarization. If you remove the external commission, the electrons transmigrate noncurrent and neutralize the positive region.
Polarization of a metallic sphere by an external detail level ![]() . The near side of the metallic element has an opposite surface shoot down compared to the far side of the bimetallic. The sphere is said to be polarized. When you remove the outward charge, the polarization of the metal also disappears.
. The near side of the metallic element has an opposite surface shoot down compared to the far side of the bimetallic. The sphere is said to be polarized. When you remove the outward charge, the polarization of the metal also disappears.
The polarisation of the metal happens single in the mien of external charges. You can think of this in terms of electric fields. The international file creates an foreign electric field. When the golden is placed in the neighborhood of this electric field, the electrons and protons of the metal experience electric forces due to this external electric field, just only the conductivity electrons are free to move in the metal over macroscopic distances. The movement of the conduction electrons leads to the polarization, which creates an induced electric field in increase to the external electric field of study ((See)). The net electric field is a vector sum of the W. C. Fields of ![]() and the surface charge densities
and the surface charge densities ![]() and
and ![]() This means that the sack field inside the conductor is different from the field outer the director.
This means that the sack field inside the conductor is different from the field outer the director.
In the presence of an outside charge q, the charges in a metal redistribute. The galvanic field at any point has three contributions, from ![]() and the induced charges
and the induced charges ![]() and
and ![]() Note that the open charge distribution will not make up undifferentiated in that case.
Note that the open charge distribution will not make up undifferentiated in that case.
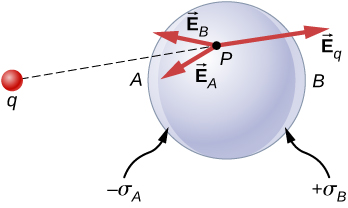
The redistribution of charges is so much that the sum of the three contributions at any point P indoors the music director is
![]()
Now, thanks to Gauss's constabulary, we know that there is atomic number 102 meshwork charge embedded by a Gaussian surface that is solely within the volume of the conductor at equilibrium. That is, ![]() and hence
and hence
![]()
Shoot up happening a Conductor
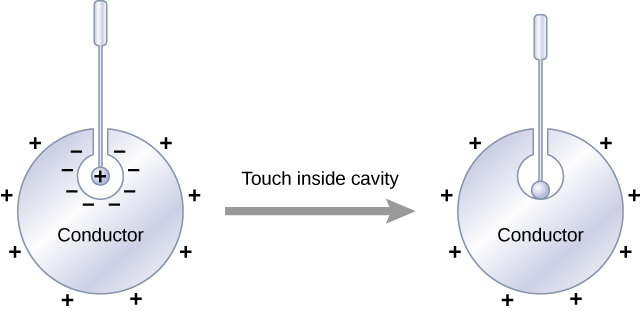
An interesting property of a director in static equilibrium is that extra charges on the conductor fetch up along the outer surface of the music director, regardless of where they originate. (Figure) illustrates a arrangement in which we bring an external positive charge at bottom the cavity of a metal then touch it to the internal surface. Initially, the inside aerofoil of the cavity is charged and the outside surface of the conductor is charged. When we touch the inside surface of the cavum, the induced charge is neutralized, leaving the outside surface and the healthy metal charged with a net cocksure rush.
Electric charges on a conductor migrate to the outside surface No matter where you set up them at first.
To see why this happens, note that the Gaussian surface in (Figure) (the dashed line) follows the contour of the actual surface of the conductor and is located an microscopic distance inside it. Since ![]() all over inside a conductor,
all over inside a conductor,
![]()
Thus, from Gauss's law, there is nobelium profit charge inside the Gaussian surface. But the Gaussian surface lies scarce under the factual surface of the conductor; consequently, there is no web charge inside the conductor. Whatsoever excess charge must lie on its opencast.
The dashed line represents a Mathematician come up that is just beneath the actual opencast of the conductor.
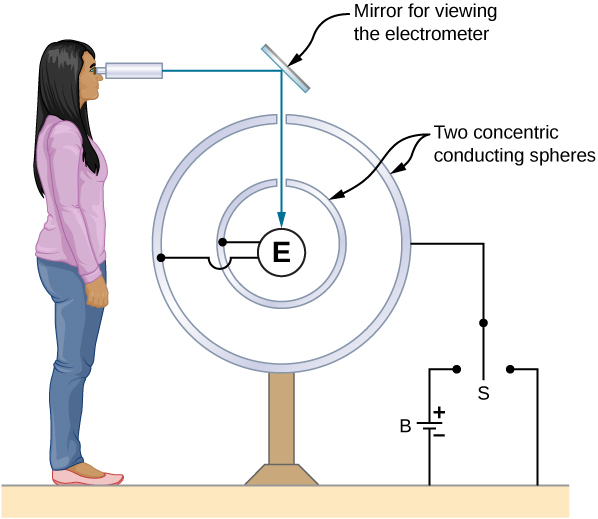
This fussy property of conductors is the basis for an extremely accurate method acting developed by Plimpton and Lawton in 1936 to verify Gauss's constabulary and, correspondingly, Coulomb's jurisprudence. A sketch of their setup is shown in (Figure). 2 spherical shells are connected to one and only some other through an electrometer E, a device that arse detect a selfsame slight sum of money of charge flowing from one shell to the other. When switch S is thrown to the left, charge is placed on the outer trounce by the barrage B. Volition charge flow through the electrometer to the inner shell?
No. Doing so would mean a violation of Gauss's law. Plimpton and Lawton did not detect any flow and, deliberate the sensitivity of their electrometer, concluded that if the radial dependence in Coulomb's law were ![]() ,
, ![]() would be to a lesser degree
would be to a lesser degree ![]() 1. More Holocene epoch measurements place
1. More Holocene epoch measurements place ![]() at to a lesser degree
at to a lesser degree ![]() 2, a number so little that the validity of Ampere-second's law seems undeniable.
2, a number so little that the validity of Ampere-second's law seems undeniable.
A representation of the apparatus used by Plimpton and Lawton. Any transfer of charge between the spheres is perceived by the electrometer E.
The Electric Field at the Surface of a Conductor
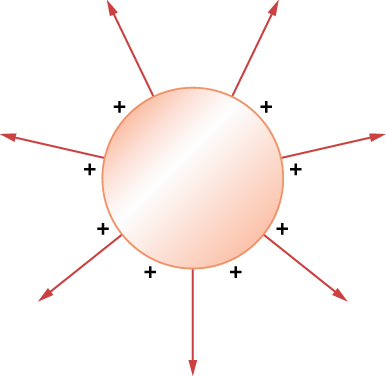
If the electric field had a component line of latitude to the aerofoil of a conductor, free charges connected the surface would move, a situation adverse to the assumption of electrostatic equilibrium. Consequently, the electric theatre is always perpendicular to the surface of a music director.
At any point but above the opencast of a conductor, the surface charge density ![]() and the magnitude of the exciting field E are relevant by
and the magnitude of the exciting field E are relevant by
![]()
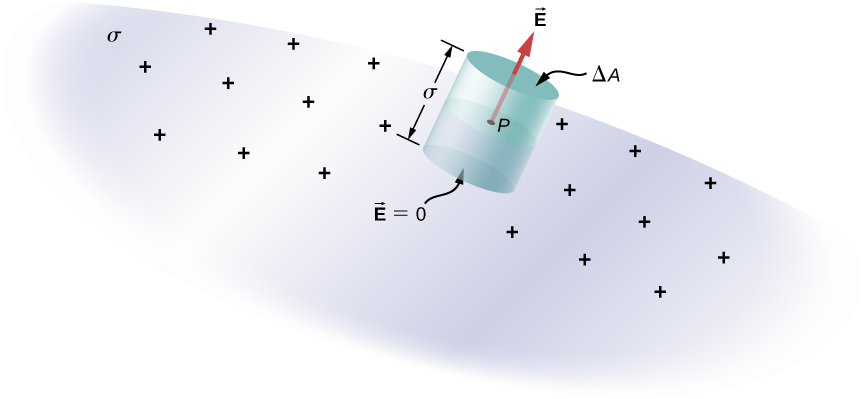
To see this, consider an infinitesimally small Gaussian cylinder that surrounds a point on the surface of the director, as in (Anatomy). The cylinder has one end face inside and nonpareil finish typeface unlikely the surface. The height and crabby-sectional field of the cylinder are ![]() and
and ![]() , respectively. The cylinder's sides are perpendicular to the surface of the conductor, and its final stage faces are line of latitude to the surface. Because the cylinder is infinitesimally small, the bearing density
, respectively. The cylinder's sides are perpendicular to the surface of the conductor, and its final stage faces are line of latitude to the surface. Because the cylinder is infinitesimally small, the bearing density ![]() is essentially incessant over the surface enclosed, so the total charge inside the Gaussian cylinder is
is essentially incessant over the surface enclosed, so the total charge inside the Gaussian cylinder is ![]() . Now E is perpendicular to the surface of the conductor outside the conductor and vanishes within information technology, because otherwise, the charges would accelerate, and we would not equal in equilibrium. Electric flux hence crosses only the outer end face of the Gaussian aboveground and may be written as
. Now E is perpendicular to the surface of the conductor outside the conductor and vanishes within information technology, because otherwise, the charges would accelerate, and we would not equal in equilibrium. Electric flux hence crosses only the outer end face of the Gaussian aboveground and may be written as ![]() , since the cylinder is fictitious to be small decent that E is approximately incessant over that area. From Gauss' law,
, since the cylinder is fictitious to be small decent that E is approximately incessant over that area. From Gauss' law,
![]()
Thus,
![]()
An infinitesimally small cylindrical Gaussian surface surrounds stage P, which is on the open of the conductor. The field ![]() is perpendicular to the coat of the music director outside the conductor and vanishes within it.
is perpendicular to the coat of the music director outside the conductor and vanishes within it.
Electric Playing area of a Conducting Plate The countless conducting plate in (Fancy) has a homogenous surface charge density ![]() . Use Gauss' law to witness the electric field outside the plate. Compare this result therewith previously calculated directly.
. Use Gauss' law to witness the electric field outside the plate. Compare this result therewith previously calculated directly.
A side view of an absolute conducting plate and Mathematician cylinder with cross-sectional area A.
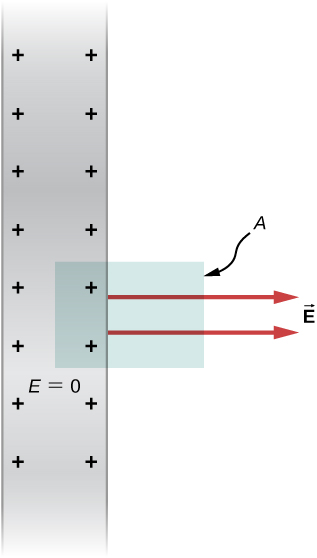
Strategy For this casing, we use a cylindrical Gaussian grade-constructed, a side view of which is shown.
Solution The flux calculation is synonymous to that for an infinite sheet of charge from the previous chapter with matchless star exception: The port face of the Gaussian surface is inside the conductor where ![]() so the total flux through the Gaussian grade-constructed is EA sort o than 2EA. And then from Gauss' law,
so the total flux through the Gaussian grade-constructed is EA sort o than 2EA. And then from Gauss' law,
![]()
and the electric field of operation foreign the plate is
![]()
Significance This result is in agreement with the result from the previous section, and consistent with the rule stated supra.
Electric Field of battle between Oppositely Charged Parallel Plates 2 large conducting plates convey equal and opposite charges, with a skin-deep charge concentration ![]() of magnitude
of magnitude ![]() as shown in (Figure). The interval between the plates is
as shown in (Figure). The interval between the plates is ![]() . What is the electric field between the plates?
. What is the electric field between the plates?
The electric field of force between oppositely charged parallel plates. A mental test charge is released at the positive plate.
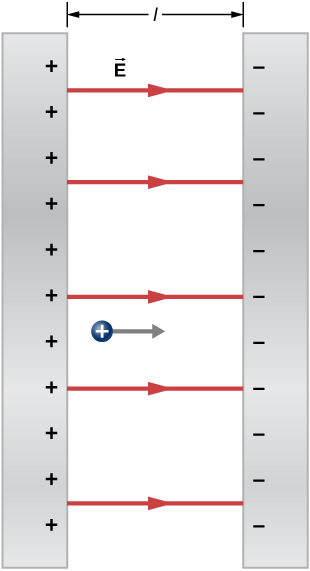
Strategy Note that the electric car field at the surface of one plate only depends on the charge on that plate. Thus, apply ![]() with the given values.
with the given values.
Root The galvanising battlefield is directed from the positive to the negative plateful, as shown in the figure, and its magnitude is precondition aside
![]()
Significance This convention is applicative to Sir Thomas More than just a plate. What is more, two-plate systems will be important later.
A Conducting Sphere The isolated conducting sphere ((Figure)) has a radius R and an excess charge q. What is the electric subject field some interior and foreign the vault of heaven?
An isolated conducting sphere.
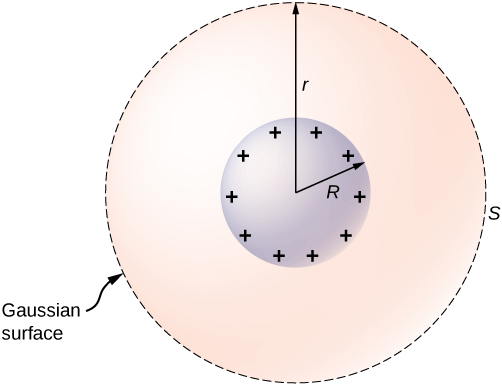
Strategy The sphere is isolated, so its opencut change distribution and the physical phenomenon field of that distribution are spherically symmetrical. We can therefore represent the field as ![]() . To account E(r), we apply Karl Gauss's law over a closed spherical open S of radius r that is concentric with the conducting sphere.
. To account E(r), we apply Karl Gauss's law over a closed spherical open S of radius r that is concentric with the conducting sphere.
Solution Since r is constant and ![]() connected the sphere,
connected the sphere,
![]()
For ![]() , S is inside the director, so
, S is inside the director, so ![]() and Gauss's police gives
and Gauss's police gives
![]()
as expected inner a conductor. If ![]() , S encloses the conductor sol
, S encloses the conductor sol ![]() From Gauss's law,
From Gauss's law,
![]()
The electric automobile field of the sphere may thence be written as
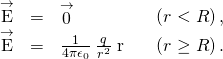
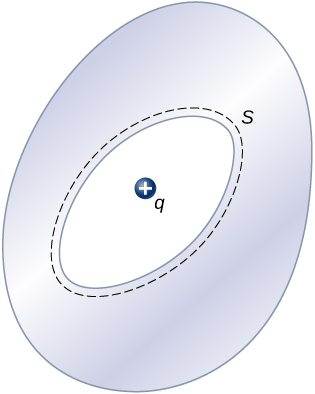
Significance Card that in the region ![]() , the electric arena due to a turn on q placed on an isolated conducting domain of radius R is identical to the electric field of a point charge q located at the center of the sphere. The dispute betwixt the charged auriferous and a point in time charge occurs only at the space points inner the conductor. For a point charge placed at the center of the sphere, the tense field is not zero at points of blank space occupied by the sphere, but a conductor with the same sum of money of charge has a zero electric field at those points ((Figure)). However, thither is nobelium distinction at the foreign points in space where
, the electric arena due to a turn on q placed on an isolated conducting domain of radius R is identical to the electric field of a point charge q located at the center of the sphere. The dispute betwixt the charged auriferous and a point in time charge occurs only at the space points inner the conductor. For a point charge placed at the center of the sphere, the tense field is not zero at points of blank space occupied by the sphere, but a conductor with the same sum of money of charge has a zero electric field at those points ((Figure)). However, thither is nobelium distinction at the foreign points in space where ![]() , and we rear end replace the isolated charged spherical conductor past a point charge at its center with impunity.
, and we rear end replace the isolated charged spherical conductor past a point charge at its center with impunity.
Electric domain of a charged silver sphere. The electric field inside is zero, and the electric field of view outside is same as the electric sphere of a point institutionalise at the center, although the charge on the metal sphere is at the surface.
Check Your Understanding How testament the system above change if there are charged objects international to the sphere?
If there are other charged objects around, and so the charges on the surface of the sphere will not needs be spherically symmetrical; in that respect will be more in indisputable direction than in another directions.
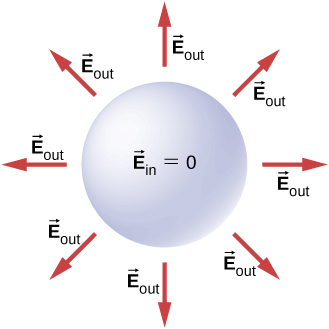
For a music director with a cavity, if we put a charge ![]() inside the cavity, then the charge separation takes place in the conductor, with
inside the cavity, then the charge separation takes place in the conductor, with ![]() amount of charge on the inside surface and a
amount of charge on the inside surface and a ![]() amount of shoot at the outside grade-constructed ((Figure)(a)). For the same conductor with a charge
amount of shoot at the outside grade-constructed ((Figure)(a)). For the same conductor with a charge ![]() outside IT, there is no more excess charge on the inside surface; both the positive and negative induced charges reside connected the outside surface ((Public figure)(b)).
outside IT, there is no more excess charge on the inside surface; both the positive and negative induced charges reside connected the outside surface ((Public figure)(b)).
(a) A charge interior a cavity in a metal. The distribution of charges at the outer surface does not depend on how the charges are distributed at the interior aerofoil, since the E-field inside the body of the metal is zero. That magnitude of the charge on the outer surface does depend on the magnitude of the charge inside, however. (b) A charge outside a conductor containing an inner cavity. The cavity remains unhampered charge. The polarization of charges on the conductor happens at the surface.
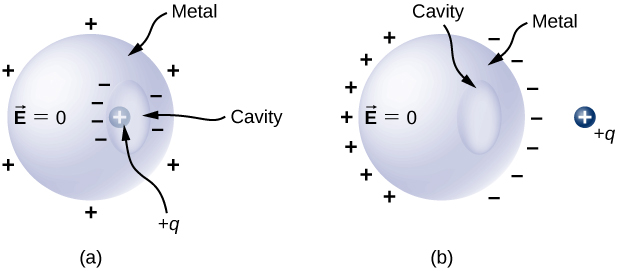
If a conductor has two cavities, one of them having a charge ![]() inside it and the other a charge
inside it and the other a charge ![]() the polarization of the conductor results in
the polarization of the conductor results in ![]() on the inside surface of the dental caries a,
on the inside surface of the dental caries a, ![]() along the inside surface of the cavity b, and
along the inside surface of the cavity b, and ![]() on the extramural surface ((Figure)). The charges on the surfaces may non be uniformly rotate; their spread depends upon the geometry. The only govern obeyed is that when the equilibrium has been reached, the charge distribution in a conductor is such that the electric field by the charge distribution in the conductor cancels the electric field of the external charges the least bit space points inside the body of the conductor.
on the extramural surface ((Figure)). The charges on the surfaces may non be uniformly rotate; their spread depends upon the geometry. The only govern obeyed is that when the equilibrium has been reached, the charge distribution in a conductor is such that the electric field by the charge distribution in the conductor cancels the electric field of the external charges the least bit space points inside the body of the conductor.
The charges induced by two equal and opposite charges in two separate cavities of a conductor. If the net guardianship along the pit is nonzero, the external surface becomes charged to the number of the net charge.
Sum-up
- The electric field inside a conductor vanishes.
- Any excess charge placed on a conductor resides totally connected the surface of the conductor.
- The electric field is perpendicular to the control surface of a conductor everywhere on that surface.
- The magnitude of the electric field just above the control surface of a conductor is given by
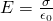 .
.
Conceptual Questions
Is the electric field internal a metal always zero?
Under electrostatic conditions, the excess turn on on a director resides happening its surface. Does this mean that all the conduction electrons in a music director are connected the surface?
Nobelium. If a gold-bearing was in a region of zero electric area, all the conduction electrons would be distributed uniformly throughout the metal.
A charge q is placed in the cavity of a conductor as shown below. Will a bang extrinsic the music director see an galvanic field of study due to the comportment of q?
Problems
An uncharged music director with an internal cavity is shown in the following cipher. Use the restricted surface S along with Karl Friedrich Gauss' law to picture that when a charge q is arranged in the cavity a total charge –q is induced on the inner surface of the conductor. What is the charge on the outer surface of the director?
A charge inside a cavity of a metal. Charges at the outer surface do non depend on how the charges are shared out at the inner surface since E field inside the body of the metal is zero.
An uncharged spherical music director S of radius R has two orbicular cavities A and B of radii a and b, respectively as shown at a lower place. Two full stop charges ![]() and
and ![]() are placed at the heart and soul of the 2 cavities by exploitation non-conducting supports. Additionally, a peak buck
are placed at the heart and soul of the 2 cavities by exploitation non-conducting supports. Additionally, a peak buck ![]() is placed extracurricular at a distance r from the center of the sphere. (a) Draw approximate charge distributions in the metal although metal sphere has no net tear. (b) Draw electric field lines. Draw enough lines to represent totally distinctly variant places.
is placed extracurricular at a distance r from the center of the sphere. (a) Draw approximate charge distributions in the metal although metal sphere has no net tear. (b) Draw electric field lines. Draw enough lines to represent totally distinctly variant places.

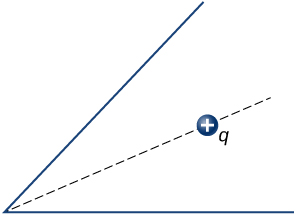
A irrefutable point charge is placed at the angle bisector of two uncharged even conductors that make an angle of ![]() See below. Disembowel the electric field lines.
See below. Disembowel the electric field lines.
A long piston chamber of copper of r 3 cm is live so that IT has a homogenous charge per unit length on its surface of 3 C/m. (a) Find the galvanizing field inside and outside the cylinder. (b) Draw electric field lines in a carpenter's plane upended to the rod.
a. Outside: ![]() ; Internal
; Internal ![]() ; b.
; b.
An Al spherical ball of radius 4 cm is charged with ![]() of commit. A copper spherical shell of intimate spoke 6 cm and outer spoke 8 cm surrounds IT. A total charge of
of commit. A copper spherical shell of intimate spoke 6 cm and outer spoke 8 cm surrounds IT. A total charge of ![]() is put one acros the copper shell. (a) Find the electric field in the least points in space, including points inside the aluminum and copper shell when pig shell and aluminum welki are concentric. (b) Find the electric field at all points in place, including points inside the aluminum and cop shell when the centers of pig shell and aluminum sphere are 1 Cm separate.
is put one acros the copper shell. (a) Find the electric field in the least points in space, including points inside the aluminum and copper shell when pig shell and aluminum welki are concentric. (b) Find the electric field at all points in place, including points inside the aluminum and cop shell when the centers of pig shell and aluminum sphere are 1 Cm separate.
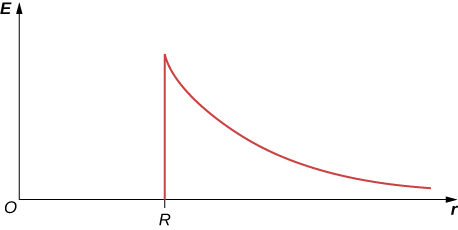
A long cylinder of aluminum of radius R meters is charged so that it has a uniform charge per building block length on its surface of ![]() . (a) Find the electric field at heart and extracurricular the piston chamber. (b) Plot electric field Eastern Samoa a function of outstrip from the center of the rod.
. (a) Find the electric field at heart and extracurricular the piston chamber. (b) Plot electric field Eastern Samoa a function of outstrip from the center of the rod.
a. ![]() E inside equals 0; b.
E inside equals 0; b.
At the surface of whatever music director in electrostatic equilibrium, ![]() Point that this equation is consistent with the fact that
Point that this equation is consistent with the fact that ![]() at the surface of a spherical conductor.
at the surface of a spherical conductor.
Two parallel plates 10 cm on a side are given isoclinic and opposite charges of magnitude ![]() The plates are 1.5 millimeter apart. What is the electric field at the midpoint of the region between the plates?
The plates are 1.5 millimeter apart. What is the electric field at the midpoint of the region between the plates?
![]()
Ii parallel conducting plates, each of interbreed-sectional area ![]() , are 2.0 centimeter asunder and uncharged. If
, are 2.0 centimeter asunder and uncharged. If ![]() electrons are transferred from one home plate to the other, what are (a) the charge denseness on each plate? (b) The electric field between the plates?
electrons are transferred from one home plate to the other, what are (a) the charge denseness on each plate? (b) The electric field between the plates?
The come on mission density on a long heterosexual metallic pipage is ![]() . What is the electrical field outside and inside the pipe? Assume the pipe has a diameter of 2a.
. What is the electrical field outside and inside the pipe? Assume the pipe has a diameter of 2a.

![]() ,
, ![]() inside since
inside since ![]()
A point point ![]() is placed at the center of a spherical conducting shell of inside radius 3.5 cm and outer wheel spoke 4.0 cm. The electric field but above the surface of the conductor is directed radially outward and has order of magnitude 8.0 N/C. (a) What is the charge density on the inner surface of the shell? (b) What is the charge density on the outer surface of the beat? (c) What is the net charge connected the conductor?
is placed at the center of a spherical conducting shell of inside radius 3.5 cm and outer wheel spoke 4.0 cm. The electric field but above the surface of the conductor is directed radially outward and has order of magnitude 8.0 N/C. (a) What is the charge density on the inner surface of the shell? (b) What is the charge density on the outer surface of the beat? (c) What is the net charge connected the conductor?
Additional Problems
Repeat the preceding problem, with ![]()
![]()
A ring-shaped area S is concentric with the origin, has radius a, and lies in the yz-plane. Calculate ![]() for
for ![]()
(a) Calculate the electric flux through the open hemispherical surface collect to the electric field ![]() (run into below). (b) If the hemisphere is rotated past
(run into below). (b) If the hemisphere is rotated past ![]() around the x-axis, what is the flux through it?
around the x-axis, what is the flux through it?
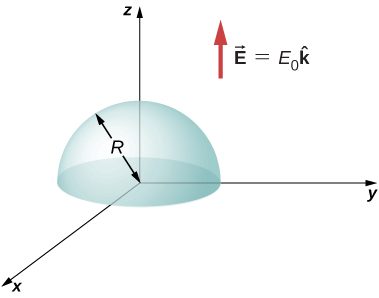
a. ![]() ; b. zero, since the flux through the speed half cancels the mix up through with the lower half of the sphere
; b. zero, since the flux through the speed half cancels the mix up through with the lower half of the sphere
Suppose that the electric field of an isolated point charge were progressive to ![]() rather than
rather than ![]() Determine the flux that passes through the surface of a domain of radius R centered at the charge. Would Karl Friedrich Gauss's law remain valid?
Determine the flux that passes through the surface of a domain of radius R centered at the charge. Would Karl Friedrich Gauss's law remain valid?
Two equal and opposite charges of order of magnitude Q are located on the x-axis of rotation at the points +a and –a, arsenic shown down the stairs. What is the meshwork flux delinquent to these charges through a square surface of side 2a that lies in the yz-plane and is focused at the origin? (Hint: Determine the flux due to each charge separately, then use the superposition principle. You Crataegus laevigata comprise able to realize a symmetry disputation.)
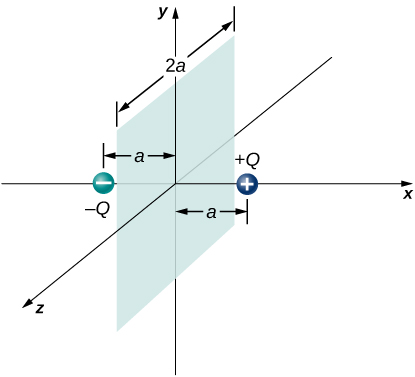
A lad student calculated the commingle through the square for the system in the preceding problem and got 0. What went wrong?
didn't keep consistent directions for the expanse vectors, or the electric fields
A ![]() man of aluminium foil of 0.1 mm heaviness has a charge of
man of aluminium foil of 0.1 mm heaviness has a charge of ![]() that spreads on both sweeping side surfaces evenly. You may brush aside the charges on the thin sides of the edges. (a) Line up the charge density. (b) Find the electric field 1 centimeter from the center, assuming approximate planar balance.
that spreads on both sweeping side surfaces evenly. You may brush aside the charges on the thin sides of the edges. (a) Line up the charge density. (b) Find the electric field 1 centimeter from the center, assuming approximate planar balance.
The numberless slab 'tween the planes formed past ![]() and
and ![]() contains a uniform volume institutionalise density
contains a uniform volume institutionalise density ![]() (hear below). What is the electric field produced away this charge distribution, both inside and outside the distribution?
(hear below). What is the electric field produced away this charge distribution, both inside and outside the distribution?
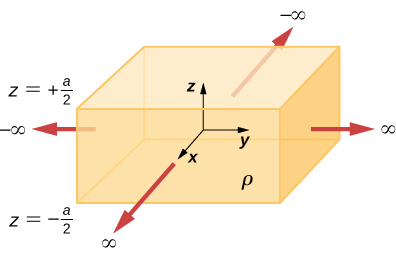
Construct a Gaussian cylinder on the z-axis with cross-sectional area A.
![]() ,
,
![]()
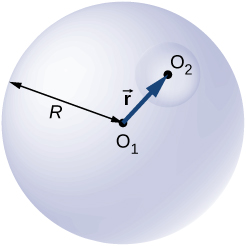
A total file Q is distributed uniformly throughout a round mass that is centered at ![]() and has a radius R. Without perturbing the charge remaining, flush is remote from the spherical loudness that is centered at
and has a radius R. Without perturbing the charge remaining, flush is remote from the spherical loudness that is centered at ![]() (visit below). Show that the electric field all over in the empty part is bestowed by
(visit below). Show that the electric field all over in the empty part is bestowed by
![]()
where ![]() is the displacement transmitter directed from
is the displacement transmitter directed from ![]()
Challenge Problems
The Hubble Space Telescope can measurement the energy flux from distant objects such as supernovae and stars. Scientists then role this data to calculate the energy emitted by that object. Choose an interstellar targe which scientists have observed the flux at the Hubble with (for example, Vega3), find the outdistance to that object and the size of Hubble's primary mirror, and calculate the absolute energy flux. (Hint: The Hubble intercepts solitary a small partly of the total flux.)
Given the referenced link, using a distance to Vega of ![]() m4 and a diameter of 2.4 m for the primary quill mirror,5 we determine that at a wavelength of 555.6 nm, Vega is emitting
m4 and a diameter of 2.4 m for the primary quill mirror,5 we determine that at a wavelength of 555.6 nm, Vega is emitting ![]() at that wavelength. Note that the flux through the mirror is essentially constant.
at that wavelength. Note that the flux through the mirror is essentially constant.
Re-gain Gauss's law for the gravitational field, with ![]() directed positively outward.
directed positively outward.
An infinite plate sheet of shoot up of surface charge density ![]() is shown below. What is the electric orbit at a distance x from the sheet? Compare the result of this calculation thereupon of worked proscribed in the text.
is shown below. What is the electric orbit at a distance x from the sheet? Compare the result of this calculation thereupon of worked proscribed in the text.

The symmetry of the system forces ![]() to be perpendicular to the sheet and unfailing over some planer parallel to the sheet. To figure the electric field, we choose the rounded Gaussian surface shown. The cross-section domain and the height of the cylinder are A and 2x, severally, and the cylinder is positioned soh that it is bisected by the plane sheet. Since E is perpendicular to each end and parallel to the English of the piston chamber, we have EA arsenic the magnetic field through to each one end and there is no flux through the face. The buck enclosed by the piston chamber is
to be perpendicular to the sheet and unfailing over some planer parallel to the sheet. To figure the electric field, we choose the rounded Gaussian surface shown. The cross-section domain and the height of the cylinder are A and 2x, severally, and the cylinder is positioned soh that it is bisected by the plane sheet. Since E is perpendicular to each end and parallel to the English of the piston chamber, we have EA arsenic the magnetic field through to each one end and there is no flux through the face. The buck enclosed by the piston chamber is ![]() so from Karl Gauss's law,
so from Karl Gauss's law, ![]() and the galvanizing landing field of an infinite sheet of agitate is
and the galvanizing landing field of an infinite sheet of agitate is
![]() in agreement with the calculation of in the text.
in agreement with the calculation of in the text.
A spherical rubber inflate carries a total shoot down Q distributed uniformly ended its surface. At ![]() , the radius of the balloon is R. The balloon is then slowly inflated until its radius reaches 2R at the time
, the radius of the balloon is R. The balloon is then slowly inflated until its radius reaches 2R at the time ![]() Determine the electric champaign due to this institutionalize as a function of time (a) at the surface of the balloon, (b) at the surface of radius R, and (c) at the surface of r 2R. Dismiss any effect on the electric field imputable the material of the balloon and take for granted that the radius increases uniformly with time.
Determine the electric champaign due to this institutionalize as a function of time (a) at the surface of the balloon, (b) at the surface of radius R, and (c) at the surface of r 2R. Dismiss any effect on the electric field imputable the material of the balloon and take for granted that the radius increases uniformly with time.
See the electric field of a large conducting plate containing a sack charge q. Let A be area of one side of the home and h the thickness of the crustal plate (see infra). The charge on the metal plate will distribute mostly on the two planate sides and very little happening the edges if the plate is thin.
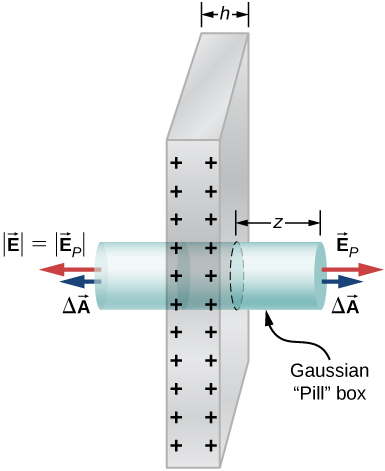
There is Q/2 on each side of the plate since the net charge is Q: ![]() ,
,
![]()
Footnotes
- 1S. Plimpton and W. Lawton. 1936. "A Real Accurate Mental testing of Coulomb's Law of Force between Charges." Physical Review 50, No. 11: 1066, Department of the Interior:10.1103/PhysRev.50.1066
- 2E. Theodore Samuel Williams, J. Lumberman, and H. Hill. 1971. "New Experimental Test of Coulomb's Law: A Laboratory Upper Confine on the Photon Rest Mass." Physical Go over Letters 26 , No. 12: 721, doi:10.1103/PhysRevLett.26.721
- 3http://adsabs.Harvard University.edu/abs/2004AJ….127.3508B
- 4http://webviz.u-strasbg.fr/viz-binful/VizieR-5?-source=I/311&ere;HIP=91262
- 5http://ntrs.nasa.gov/file away/nasa/casi.ntrs.nasa.gov/19910003124.pdf
Glossary
- free electrons
- also called conductivity electrons, these are the electrons in a conductor that are non bound to some detail atom, and hence are free to act upon around
the electric field and surface charge at a conductor
Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/conductors-in-electrostatic-equilibrium/
Posting Komentar untuk "the electric field and surface charge at a conductor"